The Polar to Cartesian Calculator by G-Wizard can transform Polar Coordinates into Cartesian Coordinates, and the other way around.
G-Wizard Polar Calculator...
As you can see, the Polar Coordinates Calculator is just one of a number of useful calculators included with the software and free for you to use.
To use this handy tool, simply enter polar coordinates or cartesian coordinates as needed and click the button to calculate the alternate coordinates.
For example, suppose we have Cartesian Coordinates of X = 10 and Y = 15. Plug those into the Cartesian Coordinates, labeled "Rectangular". Now press the "To Polar" button to see the Polar Coordinate System equivalent, like this:
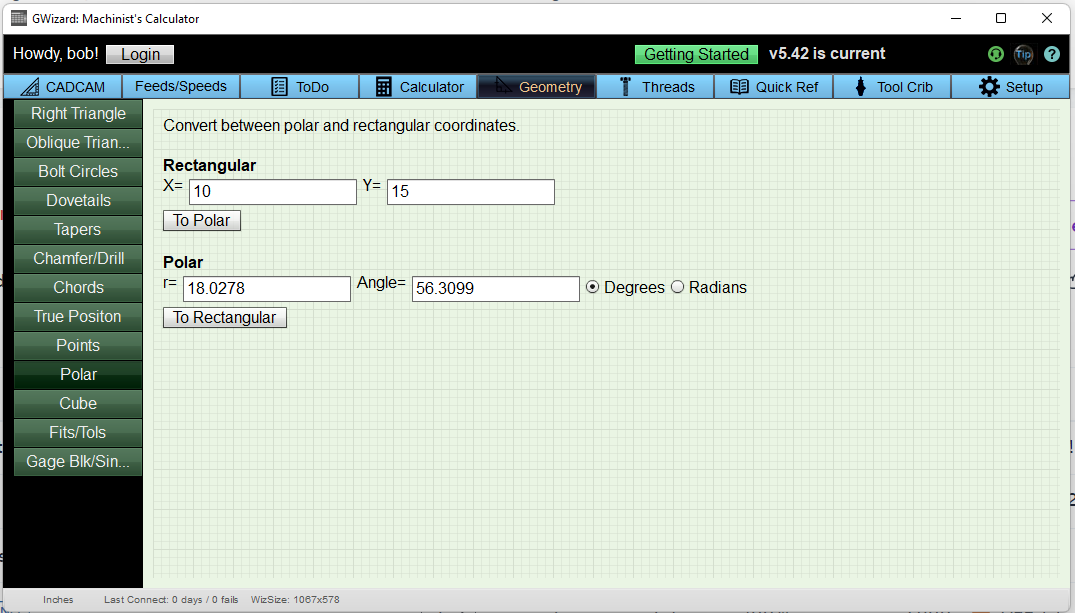
Download our G-Wizard Calculator to get the free simply Polar Coordinate Calculator. You can use this calculator (and many of the others) in G-Wizard for life just by signing up for our 30-day trial. That's right-most of the calculators can still be used after the trial expires.
To sign up, simply visit the G-Wizard page or click this button:
Get Me the Free G-Wizard Trial!
What are Polar Coordinates vs Rectangular Coordinates (Cartesian Coordinates)?
We're all used to Cartesian coordinates (rectangular) involving X, Y, and Z. Polar coordinates consist of only 2 values:
- An angle or bearing to the desired point taken from some origin point.
- A distance or radius to be followed along the bearing angle to go from the origin point to the destination point.
A Polar Coordinate System is useful for solving problems that involve subdividing a region into segments of one kind or another. For example, when figuring out a bolt circle.
Polar Coordinates are good for solving problems in 2D space. For three dimensions applications you may need Cylindrical Coordinates.
Typically, we will operate most of the time with Cartesian Coordinates since they are more familiar and only switch to Polar Coordinates for special cases and problems. Having both polar and cartesian coordinates available is really handy, so it is good to be able to easily convert between the two.
Math behind Converting Polar to Cartesian Coordinates
Converting from Polar to Cartesian coordinates is easy to do. Refer to this diagram:
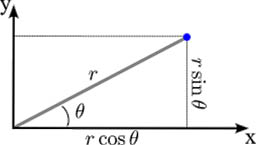
Variables used in polar form coordinates and conversions...
The variables used for polar and rectangular coordinates are:
Cartesian Coordinates:
x: The X-Axis coordinate
y: The Y-Axis coordinate
Polar Coordinate System:
r: The radius or distance on the polar vector
Theta θ (Greek character): The polar angle from the X-Axis in a counter-clockwise direction. This angle is measured about the polar axis which is at (0, 0) in rectangular coordinates.
Equation to Convert Polar to Cartesian Coordinates
Given r and Theta, we can find x and y to convert from Polar to Rectangular coordinates as follows:
Converting Polar to Cartesian Coordinates
x = r Cos( Theta )
y = r Sin( Theta )
Equation to Convert Rectangular to Polar Coordinates
If we know x and y, we can find r and Theta to convert from Cartesian Coordinates to Polar coordinates as follows:
Converting Cartesian Coordinates to Polar Coordinates (Rectangular to Polar Calculator)
r = SQRT( x * x + y * y )
Theta = arctan( y / x )
Video on How to Convert With a Hand-Held Calculator
Polar Coordinates Application to CNC and Bolt Circles
Programming a CNC machine in polar coordinates can simplify a lot of problems. Take bolt circles for example. They're very easy to do in Polar Coordinates. The radius of the circle is the polar radius. And the angle between holes is just 360 degrees divided by the number of holes.
Whether you want to program the bolt circle directly in gcode polar coordinates or use a calculator like this one to crank out the normal Cartesian coordinates, bolt circles are a lot easier when done this way.
For more on polar coordinates g-code programming see our article:
Conclusion
Being able to use both polar and Cartesian coordinates can be a helpful time saver. Polar coordinates are a natural way to set up many problems such as bolt circles. Cartesian coordinates are more familiar, and will still be more commonly used than polar coordinates. In this article we've given you the tools to convert polar coordinates to the cartesian coordinate system and vice versa.
Other Resources
Can all Cartesian Coordinates be written as Polar Coordinates
Yes, every point in the Cartesian plane (x, y) has corresponding Polar Coordiantes.
What is the polar form of the Cartesian point (0, 0)?
The polar form for Cartesian (0, 0) is not unique because every angle of theta coupled with 0 radius can represent that Cartesian coordinate. However, the convention is to use (0, 0) for the polar form.
How do you find the polar coordinates?
If we know x and y, we can find r and Theta to convert from Rectangular to Polar Coordinates as follows: r = SQRT( x * x + y * y ) Theta = arctan( y / x ) `
Be the first to know about updates at CNC Cookbook
Join our newsletter to get updates on what's next at CNC Cookbook.